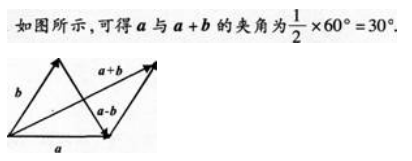
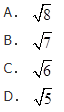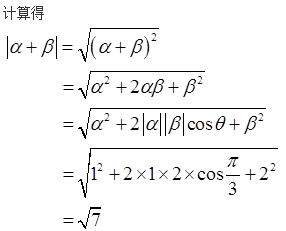已知向量a,b,c是三个具有公共起点的非零向量,且|a|=2|b|=2,又a·b=-1, 〈a-c,b-c 〉=π/3 ,则当|a-c|=7时,向量a与c的夹角是____.
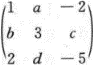,B为三阶非零矩阵,且AB=O,则r(A)=_______.
福建师范大学2021年12月常微分方程期末考核试题库及答案参考1. 某单人裁缝店做西服，每套衣服需要4道不同的工序，4道工序完工后才开始做另一套西服，每道工序所需时间所服从某单人裁缝店做西服，每套衣服需要4道不同的工序，4道工序完工后才开始做另一套西服，每道工序所需时间所服从参数4u的负指数分布，平均需要2h。又设顾客前来定制西装的过程为泊松过程，平均每周来到5.5人(每人定制一套西服，且设每周工作6天，每天工作8h)。试问一位顾客从定货到做好一套西服平均需要多少时间?2. 设cabba，且a，b，c都为非零向量，证明：c平分a与b的夹角设cabba，且a，b，c都为非零向量，证明：c平分a与b的夹角正确答案：aca(ab)b(aa)a(ab)bca(bb)b(ba)b(ba)3. 微分方程y&39;&39;-4y&39;+4y=xe2x的一个特解可设为y*=( ) Ax2e2x Bx3e2x Cx2(Ax+B)e2x De2x微分方程y-4y+4y=xe2x的一个特解可设为y*=()Ax2e2xBx3e2xCx2(Ax+B)e2xDe2xC4. 设e1，e2，en是n维欧氏空间V的一个基.证明：如果对于V中任意两个向量=a1e1+a2e2+anen，=b1e1+b2e2+bnen设e1，e2，en是n维欧氏空间V的一个基.证明：如果对于V中任意两个向量=a1e1+a2e2+anen，=b1e1+b2e2+bnen，都有，=a1b1+a2b2+anbn(6-23)则e1，e2，en是V的一个标准正交基.证 因为 ei=0e1+0ei-1+ei+0ei+1+0en (i=1，2，n). 故由题设条件(6-23)式，就有 这就是说e1，e2，en是V中的正交单位向量组，因而是V的一个标准正交基.本题连同定理6.10的(2) 说明：欧氏空间的基e1，e2，en为标准正交基对于V中任意向量，都有. 5. (哈达玛不等式)设A=detaik为n级行列式，其中之元素均为实数而合条件ak12+ak22+akn2=1，(k=1，2，n). 则(哈达玛不等式)设A=detaik为n级行列式，其中之元素均为实数而合条件ak12+ak22+akn2=1，(k=1，2，n).则必|A|1证明要应用拉格朗日乘数法来证显然本题中的辅助方程(条件方程)为 k=ak12+ak22+akn2-1=0，(k=1，2，n) 以k表乘数，置 于是从方程 得等式Ajk+jajk=0其中Ajk为A中之ajk元素所对应的子行列式 于等式两端乘以ajk并对k=1，2，n而求和，则得 A+j=0，(j=1，2，n)因之，j=-A亦即Ajk=Aajk，(j，k=1，2，n)故得出 ，亦即An-1=An+1由于A的极大极小值必须合于上列方程，故不难推知A的极大值为+1，极小值为-1因此|A|1 6. 设f(x)，g(x)在0，1上的导数连续，且f(0)=0，f(x)0，g(x)0,证明：对任何a0，1有设f(x)，g(x)在0，1上的导数连续，且f(0)=0，f(x)0，g(x)0,证明：对任何a0，1有证法1设 则F(x)在0，1上可导，并且 F(x)=g(x)f(x)-f(x)g(1)=f(x)g(x)-g(1) 由于x0，1时，f(x)0，g(x)0，表明g(x)在0，1上广义单调增加，所以F(x)0，即F(x)在0，1上广义单调减少 注意到 而故F(1)=0 因此，x0，1时，F(x)0,由此可得对任何a0，1，有 证法2 因为所以 又由于x0，1时，f(x)0，所以f(x)在0，1上广义单调增加，则有f(x)f(a)，对于任意xa，1 又由题设，当x0，1时，有g(x)0，所以 f(x)g(x)f(a)g(x)，xa,1于是 从而 注 在证法2中，证明“”时用到了f(x)的单增性和积分性质,在这一步骤中，可以用积分中值定理，具体证明如下： 由积分中值定理知，存在a，1，使 一般来说，有关定积分的等式或不等式的证明，可将某一积分上限换成x，从而将问题转化为一个有关函数的等式或不等式问题，再通过研究该函数的性态来达到证明的目的，如果用该思路来证明本问题，可考查考生对定积分变上限函数的导数的理解和计算以及利用导数判断函数单调性的掌握，另外，通过对不等式左边的两个被积函数形式的考察，可以想到用定积分的分部积分法来变形，所以本题一般可用以下两种方法证明 7. 设A是n(n1)阶矩阵，满足Ak=2E(k2，kZ+)，则(A+)k=( )A(1/2)EB2EC2k-1ED2n-1E设A是n(n1)阶矩阵，满足Ak=2E(k2，kZ+)，则(A+)k=( )A(1/2)EB2EC2k-1ED2n-1E正确答案：D8. 函数y=tan2x+cosx是一个非奇非偶的周期函数。( )A.正确B.错误参考答案：A9. 直线y=2x，y=x/2，x+y=2所围成图形的面积为( )A.2/3B.3/2C.3/4D.4/3参考答案：A10. 若同构的群认为是相同的，那么3阶群有_个，4阶群有_个若同构的群认为是相同的，那么3阶群有_个，4阶群有_个1$211. 函数在f(x)在x处有定义，是当xx时f(x)有极限的充分必要条件。( )A.错误B.正确参考答案：A12. 给定三点Ai(xi，yi)，i=1，2，3 求证按最小二乘拟合这三点的直线过A1A2A3的重心给定三点Ai(xi，yi)，i=1，2，3 求证按最小二乘拟合这三点的直线过A1A2A3的重心记，则为A1A2A3的重心 设拟合直线为 y=a+bx， (5.7) 则a，b满足正规方程组 其中s0=3，考虑第一个方程 两边同除以3得，即点在直线(5.7)式上因而按最小二乘拟合三点Ai(i=1，2，3)的直线过A1A2A3的重心 13. 二阶无零元素的行列式等于零的充要条件是其两行对应元素成比例( )二阶无零元素的行列式等于零的充要条件是其两行对应元素成比例()正确14. 下列函数f(x)在x=0处是否连续？为什么？ (1) (2) (3) (4)下列函数f(x)在x=0处是否连续？为什么？(1)(2)(3)(4)依题意，只用检查是否成立 (1)因x0时，x2为无穷小量，为有界量，故其积为无穷小量，从而故f(x)在x=0处连续. (2)因x0时，从而 故f(x)在x=0连续 (3)f(x)在x=0的左、右极限不相等： ， 故f(x)在x=0处不连续. (4)因为 ， 即，又f(0)=e0=1，故f(x)在x=0连续 15. 已知某产品的净利润P与广告支出x有如下的关系：Pba(xP) 其中a、b为正的已知常数，用P(0)P。0已知某产品的净利润P与广告支出x有如下的关系：Pba(xP) 其中a、b为正的已知常数，用P(0)P。0 求PP(x)正确答案：16. 偏序集合的哈斯图一定是一个连通图( )偏序集合的哈斯图一定是一个连通图()错误17. 极值反映的是函数的( )性质。A.局部B.全体C.单调增加D.单调减少参考答案：A18. y=cos(1/x)在定义域内是( )。A.周期函数B.单调函数C.有界函数D.无界函数参考答案：C19. 分别按下列条件求平面方程：分别按下列条件求平面方程：可取该平面的法向量为j=(0，1，0)，于是所求平面方程为y+5=0$可先设该平面方程为Ax+By=0，以(-3，1，-2)代入，得-3A+B=0，即B=3A，代入上面方程并消去A，所求方程为x+3y=0$记M1(4，0，-2)，M2(5，1，7)，则该平面的法向量n，且nOx，而=(0，9，-1)，所以=(0，9，-1)，于是所求平面方程为9(y-0)-(z+2)=0，即9y-z-2=020. 设函数f(x-2)=x2+1，则f(x+1)=( )A.x2+2x+2B.x2-2x+2C.x2+6x+10D.x2-6x+10参考答案：C21. 证明：Gauss整环Zi关于映射 ：a+bia2+b2作成一个欧氏环证明：Gauss整环Zi关于映射 ：a+bia2+b2作成一个欧氏环正确答案：显然对任意Zi有rn ()=|2 ()=()()rn故当0时令-1=s+ti(stQ)且ab分别是最接近st的整数于是q=a+biZi且rnrn从而由上知：rn (-1-q)=(s-a)2+(t一b)2 (1)rn再令r=-q则r=0或由(1)有rn (r)=(-q=()(-1一q)rn因此Zi关于作成一个欧氏环显然,对任意,Zi,有()=|2,()=()()故当0时,令-1=s+ti(s,tQ)且a,b分别是最接近s,t的整数于是q=a+biZi,且从而由上知：(-1-q)=(s-a)2+(t一b)2(1)再令r=-q,则r=0,或由(1)有(r)=(-q=()(-1一q)因此,Zi关于作成一个欧氏环22. R为含幺环，a，bR，且a-1，b-1R，证明：(ab)-1=b-1a-1R为含幺环，a，bR，且a-1，b-1R，证明：(ab)-1=b-1a-1(ab)(b-1a-1)=a(bb-1)a-1=aa-1=1 (b-1a-1)(ab)=b-1(a-1a)b=b-1b=1 于是b-1a-1是ab的逆元，即(ab)-1=b-1a-1 23. 两个无穷大量的和仍是无穷大。( )A.错误B.正确参考答案：A24. 设A，BAB-E是同阶可逆矩阵，则(A-B-1)-1-A-1)-1等于( )
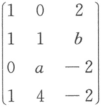,且存在三阶非零矩阵B,使得AB=O,则a=_______,b=_______.
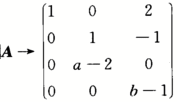，因为AB=O，所以r(A)+r(B)≤3，又B≠O，于是r(B)≥1，故r(A)≤2，从而a=2，b=1.
