A、P(X+Y≤0)=1/2
B、P(X-Y≤0)=1/2
C、P(X+Y≤1)=1/2
D、P(X-Y≤1)=1/2
假设X～N(-1,2),Y～N(1,3)，且X与Y相互独立，则X+2Y～
A、N(1,8)
B、N(1,14)
C、N(1,40)
D、N(1,22)
好莱坞3位动作巨星G、H和I将在一次晚会上表演6个高难度动作O、P、T、X、Y和Z。这些动作将被连续表演，且每个动作只表演1次。表演遵循以下条件。
(1) Y必须在T和O的前面表演。
(2) P必须在Z之前在O之后表演。
(3) G仅可以表演X，Y和Z。
(4) H仅可以表演T，P和X。
(5) L仅可以表演O，P和X。
(6) 表演第1个动作的人不能表演最后1个动作。
下面哪一项是一个可以接受的从前到后的动作表演顺序?
A．X，T，Y，O，P，Z
B．X，Z，Y，T，O，P
C．Y，O，P，X，T，Z
D．Y，X，O，P，Z，T
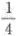,则P（X>1,Y>-2）=_______.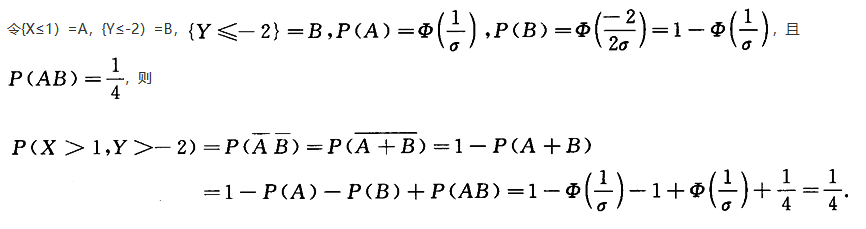
，故
.第一章 第二章 第三章 第四章 第五章、t r ; 弟八早 第七章第八章 第九章 第十章高等代数（北大第三版）答案目录多项式行列式线性方程组矩阵二次型线性空间线性变换矩阵欧氏空间双线性函数与辛空间注：答案分三部分，该为第二部分，其他请搜索，谢谢！12.设A为一个n级实对称矩阵，且 A 0,证明：必存在实 n维向量X 0,使XAX 0。n ,且A不是正定矩阵。故必存在非证 因为A 0 ,于是A 0,所以rank A退化线性替换X C 1Y使X AX Y C 1 ACY YBY2yi2V22222ypyp i yp 2yn,且在规范形中必含带负号的平方项。于是只要在yp0, yp 1 yp 2yni,则可得一线性方程组 TOC o 1-5 h z CiiXiC12X2CinXn0Cp1X1Cp2 x2Cpnxn 0Cp 1,1X1 Cp 1,2X2C p 1,n Xn1CniXi Cn2X2gn Xn1由于C 0 ,故可得唯一组非零解Xsx1s,x2s,Xns使sis， as，nsXsAXs 0 00 1 11 n p 0,即证存在X 0 ,使X AX 0。13 .如果A, B都是n阶正定矩阵，证明： A B也是正定矩阵。证 因为A,B为正定矩阵，所以 X AX, X BX为正定二次型，且XAX 0,XBX 0,因此X A B X X AX X BX 0,是X A B X必为正定二次型，从而A B为正定矩阵。14 .证明：二次型f Xi,X2, ,Xn是半正定的充分必要条件是它的正惯性指数与秩相等。证 必要性。采用反证法。若正惯性指数若令则可得非零解0矛盾，故充分性。2f X1 , X2 , Xny1y1 y2yp 0，ypX1 , X2 , XnXi, X2,f X1, X2 , Xn2y1故有 f X1, X2 , Xn15 .证明:n2n Xii1nnX；i1可见:2X11)2)2y2, Xn2y20 ,即证二次型半正定。Xii12n X12X22X22X2Xn2X12X222yp yp 1y1 ，0。这与所给条件X1 , X2 , X nX12 2 X1X 2nXii12Xn2x1x22Xn 1 Xn )2是半正定的。2 X1 Xn2x2 X32X2 Xn2Xn 1Xn2Xn2x1 x22 X1 X n2X2X322X2X12 X1X 32XiXj oi j nX1 , X2 ,X1X2,Xn不全相等时X1, X2 , XnXn时X1 , X2 , Xn2X3XinXjXiXj2Xn 10。0。2Xn 1 Xn2Xn故原二次型f x1,x2,Xn是半正定的。16 .设f X1,X2, ,XnXAX是一实二次型，若有实 n维向量Xi,X2使 TOC o 1-5 h z X1Ax 0, X2AX20。证明：必存在实n维向量X00使X0AX00。设A的秩为r ,作非退化线性替换 X CY将原二次型化为标准型 222XAX diyi d2y2drYr ,其中dr为1或-1。由已知，必存在两个向量 Xi,X2使XiAXi 0 和X2AX2 0,故标准型中的系数d1,dr不可能全为1,也不可能全为-1。不妨设有p个1, q个-1 ,2222xax y yp ypiypq,这时p与q存在三种可能：p q， p q， p q下面仅讨论p q的情形，其他类似可证。令yiyq 1,yq 1yp , ypiyp q 1,则由Z CY可求得非零向量 X0使 2222X0AX0yiypypiyp q0,即证。A是一个实矩阵，证明：rank A A rank A 。0与AAX 0为同解方程组，故只要证 由于rank A rank AA的充分条件是 AX证明AX 0与A AX 0同解即可。事实上AX 0 AAX 0X A AX 0AX AX 0即证AX 0与AAX 0同解，故rank A A rank A 。注 该结论的另一证法详见本章第三部分（补充题精解）第 2题的证明，此处略。一、补充题参考解答.用非退化线性替换化下列二次型为标准型，并用矩阵验算所得结果:1) XnX2X2n 1X2X2n 1XnXn 1 ；22y1y2Ynyn 122Y2n 1 y2n ,2)X1X2X2X3XnXn；nX：Xi Xj ;11 i j n八 n2X1X2XnXi X ,其中 X 1n解1 )作非退化线性替换X1y1y2 nX2y2y2n 1Xnynyn 1Xn 1y nyn 1且替换矩阵其中2）若T ATy1X1X2X3y2X1X2X32 y12y2y1y2y1y2于是当n为奇数时，作变换X1X2X2X3,VXix 1 Xi 2XXi iXi 2i 1,3,5, ,n 2 ,YnXnX1X2X2X3Xn 1 Xn2222Y1Y2Y3Y422Yn 2Yn111000111000111000111000且当n 4k 1时，得非退化替换矩阵为1111 TOC o 1-5 h z HYPERLINK l bookmark331 o Current Document 1100 HYPERLINK l bookmark91 o Current Document 11T11当n 4k 3时，得非退化替换矩阵为1111 HYPERLINK l bookmark206 o Current Document 1100 HYPERLINK l bookmark349 o Current Document 11T11 HYPERLINK l bookmark87 o Current Document 1101故当n为奇数时，都有1111TAT当n为偶数时，作非退化线性替换XiXi 1 Xi 2VXi 1Xi 22Xn 1 XnYn 1Xn 1 XnynX1X2X2X3i 1,3,5, ,n 3 ,2222Xn 1Xn Y1Y2Y3Y422Yn 1Yn,于是当n 4k时，得非退化替换矩阵为1111111100001111T1100于是当n 4k 2时，得非退化替换矩阵为1111 HYPERLINK l bookmark543 o Current Document 110011T11故当n为偶数时，都有 HYPERLINK l bookmark377 o Current Document 11 HYPERLINK l bookmark172 o Current Document 00 HYPERLINK l bookmark523 o Current Docume、nt 11 HYPERLINK l bookmark180 o Current Document 00TAT3）由配方法可得f于是可令X1X2xj j 321 n 1 2xn 1 - xnxn ,n 2ny1x1y2 x22jxj23jxj31 yn 1 n y nn 1- xnnyn xn则非退化的线性替换为13y3 TOC o 1-5 h z 1 x1y1- y221x2y23 y311yn 1- y nn 1 n1xn 1yn 1 y nn且原二次型的标准形为2y13 24y2n 2FT yn2n相应的替换矩阵为11111123n1n111013n1n11001n1n00011n0000、1又因为所以4）令TATyi xi xy2 x2 xyn 1 xn 1 x y nxn则nxi 2yiVi 2nx2yi 2y2 Vi 3n 2 xn iyi 2yn i yni ixnYn由于yixin i原式 y2i i HYPERLINK l bookmark80 o Current Document nn i2ynyyii ii iyi i in i 22 V yii ii i j n i3 2 Z22zn i2z23 22Z2其中所作非退化的线性替换为 TOC o 1-5 h z 111YlZi-Z2-Z3一； Zni23n 1111y2Z2- Z3Z4-Zn134n 1y n 1Z
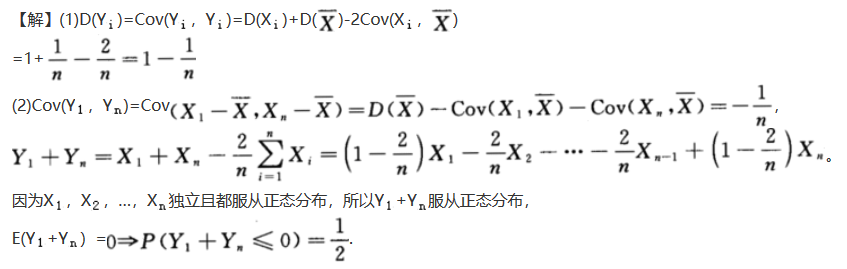
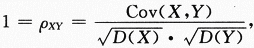
，也可得到a=2