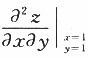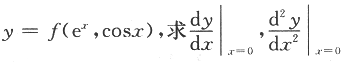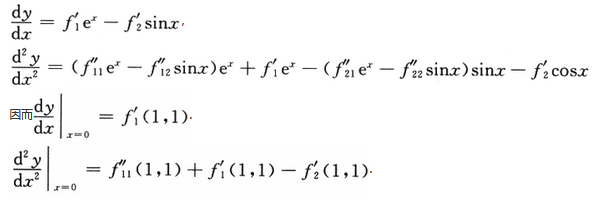设f(x)在[0，1]上可导，且满足f(1)=∫01xf(x)dx，证明：必有一点ξ∈(0，1)，使得ξf(ξ)+f(ξ)=0．
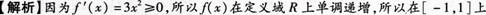
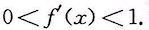
第十一讲研究生入学试题选讲一厦大2004 年考题1。判断题：(1)设nx为实数列，若nx不趋于无穷大，则nx必存在收敛的子列。（正确）证明：因为nx不是无穷大，所以0,nBNnN xB，对11111,nNnNxB，对22222,nNnNxB，对,kkkknNknNxB，从而得到nx的一个收敛的子列knx，由致密性定理knx有收敛的子列klnx，即nx存在收敛的子列。(2) 设 函 数( )f x在 非 空 开 区 间( , )a b内 有 连 续 导 数 ， 则12121212()()( , ),( , ),( )f xf xa bx xa bxxfxx。（不正确）反例：设3( )f xx在( 1,1)内有连续导数，0( 1,1),( )0f，但33221212121211221212()(),( 1,1),0f xf xxxx xxxxx xxxxxx。(3)设函数( )fx在区间0,1上有定义， 且极限11lim( )nnkkfnn存在，则此时( )f x在0,1上可积，且1101( )lim()nnkkf x dxfnn。 （不正确）反例：11,1( )( ),( )1,()11()0,nkxQkkf xD xffnxQnnn， 但( )f x在0,1上不可积。(4)设函数级数1( )nnfx在有限区间(,)I上一致收敛，且1( )nnfx收敛，则1( )nnfx在I上必一致收敛。 （不正确）反例：令1( ),( )( 1) ,( )( )( ),0,1nnnnnnnnaxxxb xfxax b xx。0,10,10,10,1, lim( )0,max( ),1sup( )0sup () (1)0()11nnnxnnxxnxaxaxnnnaxnnn所以，( )nax在0,1上一致收敛于零。 又对于固定的0,1x，( )nax单调减少；0,( )1nkknNbx，由狄里克莱判别法，0( )nnfx在0,1一致收敛。又1( )0,1),( )(1),1,( )nnnnfxxfxxxxfx1x时，(1)0nf，所以0( )nnfx在0,1收敛。但00( )(1)nnnnfxxx在0,1非一致收敛。事实上，它的和函数0,1( )1,0,1)xs xx在0,1不连续，所以，它在0,1非一致收敛。(5)设(, )X d为一个度量空间，AX为一个非空集合，A为闭集的充要条件是,xX若( ,)inf( , );0d x Ad x aaA，则.xA。（正确）证明：必要性：设A为闭集，则dAA。现用反证法。若,xX( ,)inf( , );0d x Ad x aaA，但xA。由下确界定义，000, ( ,)aA d x a，又A为闭集且xA，所以0( ,)0d x a。取11111,0( ,)1aAd x a，取2122211min( ,),0( ,)22d x aaAd x a，取111min( ,),0( ,)nnnnnd x aaAd x ann，。从而得一数列na，(),nnmax nnmaa。所以，x为A的聚点，即dxAxA，与假设矛盾。 所以假设不成立，即有,xX若( ,)inf( , );0d x Ad x aaA，则.xA。充分性：dxA，则,()nnaA ax n，从而有0( ,)inf( , );( ,)0()nd x Ad x a aAd x an，所以，( ,)0d x A，由条件，dxAAA，所以A为闭集。2求下列极限（1）limnna，其中1111 ,nan重根号。解：1211,112,1,nnaaaa。易证na单调增加有上界2，所以极限存在。设limnnal，则在递推式中令n，得，1ll，由极限保号性，解得152l。（2）222200lim()x yxyxy解：222200lim()x yxyxy422422c o ss i n2s i nc o s2s i nc o sl n000lim()lim1xrtyrtrttrttrrrree。3 设( )f x在 ,)a二阶可微， 且( )0,( )0,f afa当xa时，0f证明：方程( )f x=0 在 ,)a内有唯一实根。4设有界函数( )f x在 , a b上可积，且( )0baf x dx，证明：在( )f x的连续点处有( )f x=0。5讨论级数211ln(1)(0)npnxnpnn的敛散性。6设( , )zz x y满足22220zzzxy，作满足uvvu的变换( , )( , )xu vyu v，证明：此时也有22220zzuv。7若函数( , )uu x y z在某一区域内具有二阶的连续导数，且满足2222220uuuuxyz，则称( , , )uu x y z为该区域内的调和函数。证明：若( , , )uu x y z为区域32222000( , )()()()x y zRxxyyzza内的调和函数，则00021(,)( , , )4Su xy zu x y z dsa，其中0,a为常数， S 为球的球面。二厦大2005 年考题1。判断题：（1）函数( )f x在某点0 x连续的充分必要条件为：对任何收敛到0 x的数列nx，数列()nf x均收敛。（不正确）反例：设,0( )1,0 xxf xx，:0(),0,()0()nnnnnxxnxf xxn，但( )f x在 0点不连续。（2）函数( )f x定义在( , )a b上， 则( )f x在0( , )xa b处连续的充分必要条件为：0 00 0lim( )lim( )mM其中00(,)( )inf( )xxxmf x，00(,)( )sup( )xxxMf x。 （正确）证明：令( )( )Mm。0( , )xa b充分性：000(,),( )()xxxf xf x，且000 xx，由条件，0 0lim0，所以，00000 00lim( )()lim0lim( )()xxxxf xf xf xf x， 即( )f x在0( , )xa b处连续。必要性：若( )fx在0( ,)xa b处连续，则000,0,:,( )()xxxf xf x。从而1200121020,(,),()()()()()()2x xxxf xf xf xf xf xf x所以，0 02 ,lim0，即0 00 0lim( )lim( )mM。（3）设( )f x是n次多项式，则,a xR都有2( )()()( )( )()( )( )( )2!nnxaxaf xf axa fafafan。（正确）因为(1),( )0nxR fx，由泰勒公式即得此式。（4）设( )f x在( , )a b上导数处处存在， ,( , )c da b，由中值定理，( ,)( ,),c dc d使得( )( )( )()f df cfdc， 则( , )c d是关于,()( , )c d cda b的连续函数。 （不正确）因为( )( )( )f df cfdc中的不唯一。（5）当函数( )f x在 , a b上 R 可积时，1( )lim( )bnnkabakf x dxfnn。（不正确）因为kn不一定属于 , a b，如取2,3,2,3kabn。上式只有取0,1ab时成立。2设01151,(),1,2,2nnnxxxnx，证明：limnnx存在，并求之。3证明：若函数( )fx在区间0, l上连续及当0l时，222()0 xyz， 则函数2220( )( , , )()lfdu x y zxyz满足拉普拉斯方程2222220uuuxyz。4 设1( )nnnf xa x的收敛半径为， 令1( )nknkkfxa x， 证明：( )nffx在任何有限区间 , a b上都一致收敛于( )ff x。5设函数( )f x在 , a b上 R-可积，证明：存在 , a b上的多项式函数列( )(1,2,)nx n使得lim( )( )bbnnaax dxf x dx。6计算：2212CXdYYdXIXY，其中,XaxbyYcxdy，C为包围原点的简单闭曲线（0)adcb。三福大2004 年考题1 设0nx，证明：nx为无穷小量的充要条件是1nx为无穷大。2 设41sin,0( )0,0 xxf xxx，求(0)f。3 证明：当02x时，2sinxxx。4 证明： 奇函数的一切原函数皆为偶函数，偶函数的原函数中有一为奇函数。5 计算星形线33cos ,sinxat yat的周长。6 设1nnna b收敛，12nnsaaa，证明：级数11()nnnns bb收敛的充要条件是数列nns b收敛。7 讨论2201( )f ydxxy在0y的一致收敛与连续性。8 设方程组sinsinxyuvxvyu，确定可微函数( , )( , )uu x yvv x y，试求,uudvxy。9 计算曲线积分11(ln)(ln)CIdxdyyrxr，其中22rxy，C为平面上任意一条不过原点的简单光滑闭曲线，取逆时针方向。10计算曲面积分333SIx dydzy dzdxz dxdy， 其中 S为整个球面2222(0)xyzax a的外侧。四福大2005 年考题1 设limnnxa，证明：12limnnxxxan。2 设00()0,()0fxfx，证明： 必存在0 x的一个去心邻域，使得在此去心邻域内0( )()f xf x。3 计算下列各题（1）210sinlim()xxxx；（2）ln,xxdxR。4 设(0)0,(0)ff存在，定义数列22212()()()nnxffnnn，证明：1lim(0)2nnxf。5 证明：若( )f x在 , a b上连续，且( )( )0bbaaf x dxxf x dx，则至少存在两点12,( , )x xa b，使得12()()0f xf x。6 设11,nnnnuv为两正项级数，lim0nnnuv，证明：当1nnv收敛时，1nnu也收敛；又若1nnv发散时，1nnu如何？7 证明：1nxnne在(0,)内连续。8 设222222221()sin,0,( , )0,0.xyxyxyf x yxy证明：( , ),( , )xyfx yfx y存在且不连续， 在（0，0）点的任何邻域无界，但( , )f x y在（ 0，0）点可微。9 求球面2222xyza含在柱面22,(0)xyax a内部的面积。10求(sin)(cos)xxAMOeymy dxeym dy，其中AMO为由A( ,0)a至 O(0,0)，经上半圆周22,(0)xyax a的道路。五上海交通大学2004 年考题1设limnnaa，证明：1222lim2nnaanaan。2. 证明：2sin()x在0,)不一致连续。3设( )f x在0,2a上连续，且(0)(2 )ffa。证明：00,xa，使得00()()f xf xa。4证明：当02x时，2sinxxx。5设( )a、f x dx收敛，且( )f x在 ,)a上一致连续，试证明：lim( )0 xfx。6设121211,1,2,nnnnxxdx nnx，证明级数11( 1)nnnx收敛。7设( )f x在0,1连续，(1)0,( )( ),1,2,nnfgxf x xn，证明：( )ngx在0,1上一致收敛。8设( )f x在0,1连续，证明：10lim( )(1)nnn x f x dxf。9设1110,nnnaaaa，证明：lim12nnan。10计算下列积分：（1）2Dyx dxdy，其中 D 是矩形区域：1,01xy。（2）22()Syzdydzxzdzdxxydxdy， 其中 S 是曲面224yxz上0y的那部分正側。六福师大2004 年考题1 试确定常数,a b，使22020limsinxtxaxxb edtxx为有限值，并求此极限。2 设n为自然数，01x，证明：1(1)nxxne。3 设函数222222ln(),0( , )0,0 xyxyxyf x yxy，试求：( , ),( , )xyfx yfx y，并讨论( , )f x y在（ 0，0）的可微性。4 求级数1(21)!nn
=________.
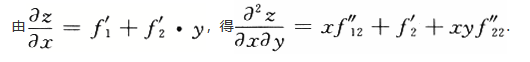
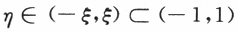
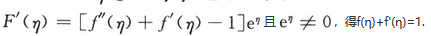
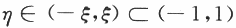，使得F'(η)=0.即f(η)+f'(η)-1=0
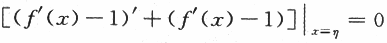，因此，应考虑辅助函数F(x)=［f'(x)-1]e^x；另一种思路是欲证f(η)+f'(η)=1，只要证f(η)+f'(η)-1=0，因此，应考虑辅助函数F(x)=f'(x)+f(x)-x.
