【证明】(Ⅰ)因为f(x)是区间[-1,1]上的奇函数,所以f(0)=0.
因为函数f(x)在区间[0,1]上可导,根据拉格朗日中值定理,存在ξ∈(0,1),使得
f(1)-f(0)=f'(ξ).
又因为f(1)=1,所以f'(ξ)=1.
(Ⅱ)【证明】(方法一)因为f(x)是奇函数,所以f'(x)是偶函数,故f'(-ξ)=f'(ξ)=1.
令F(x)=[f'(x)-1]e^x,则F(x)可导,且F(-ξ)=F(ξ)=0.
根据罗尔定理,存在
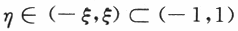
使得F'(η)=0.
由
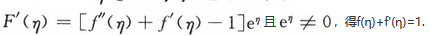
(方法二)因为f(x)是[-1,1]上的奇函数,所以f'(x)是偶函数,
令F(x)=f'(x)+f(x)-x,则F(x)在[-1,1]上可导,且
F(1)=f'(1)+f(1)-1=f'(1)
F(-1)=f'(-1)+f(-1)+1=f'(1)-f(1)+1=f'(1)
由罗尔定理可知,存在η∈(-1,1),使得F'(η)=0.
由F'(x)=f(x)+f'(x)-1,知
f(η)+f'(η)-1=0,f(η)+f'(η)=1.
(方法三)因为f(x)是[-1,1]上的奇函数,所以f'(x)是偶函数,f(x)是奇函数,由(Ⅰ)知,存在ξ∈(0,1),使得f'(ξ)=1.
令F(x)=f'(x)+f(x)-x,则F'(x)=f(x)+f'(x)-1,
F'(ξ)=f(ξ)+f'(ξ)-1=f(ξ)
F'(-ξ)=f(-ξ)+f'(-ξ)-1=-f(ξ)
当f(ξ)=0时,f(ξ)+f'(ξ)-1=0,即f(ξ)+f'(ξ)=1.结论得证.
当f(ξ)≠0时,F'(ξ)F'(-ξ)=-[f(ξ)]^2<0,
根据导函数的介值性,存在
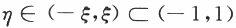
,使得F'(η)=0.即f(η)+f'(η)-1=0
故f(η)+f'(η)=1.
【评注】本题是一道微分中值定理的证明题,其难点在于(Ⅱ)中辅助函数的构造.欲证f(η)+f'(η)=1,只要证f(η)+(f'(η)-1)=0,即
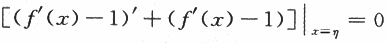
,因此,应考虑辅助函数F(x)=[f'(x)-1]e^x;另一种思路是欲证f(η)+f'(η)=1,只要证f(η)+f'(η)-1=0,因此,应考虑辅助函数F(x)=f'(x)+f(x)-x.
方法三中用到达布定理即(导函数的的介值性),这个定理不是<考试大纲》要求的考试内容,部分考生给出了此种解法,只要书写正确,不影响得分.
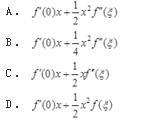
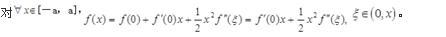

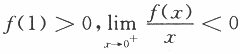 ,证明:
,证明:
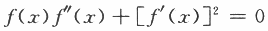 在区间(0,1)内至少存在两个不同实根.
在区间(0,1)内至少存在两个不同实根.
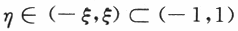
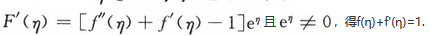
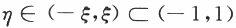 ,使得F'(η)=0.即f(η)+f'(η)-1=0
,使得F'(η)=0.即f(η)+f'(η)-1=0
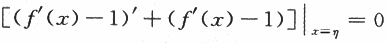 ,因此,应考虑辅助函数F(x)=[f'(x)-1]e^x;另一种思路是欲证f(η)+f'(η)=1,只要证f(η)+f'(η)-1=0,因此,应考虑辅助函数F(x)=f'(x)+f(x)-x.
,因此,应考虑辅助函数F(x)=[f'(x)-1]e^x;另一种思路是欲证f(η)+f'(η)=1,只要证f(η)+f'(η)-1=0,因此,应考虑辅助函数F(x)=f'(x)+f(x)-x.
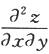 =________.
=________.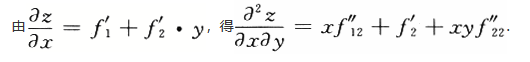

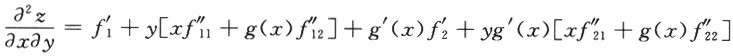

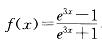 ,则:
,则:
