已知系统微分方程和初始条件为y″（t）+2y′（t）+y（t）=f（t），y（0-）=0，y′=（0-）=2，则系统的零输入响应为（）
第1题：
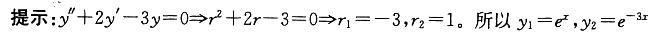B的特解，满足条件。第2题：
第3题：
有一线性系统，其输入分别为u1(t)和u2(t)时，输出分别为y1(t)和y2(t)。当输入为a1u1(t)+a2u2(t)时(a1,a2为常数)，输出应为()。
A.a1y1(t)+y2(t)
B.a1y1(t)+a2y2(t)
C.a1y1(t)-a2y2(t)
D.y1(t)+a2y2(t)
第4题：
第5题：
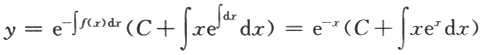
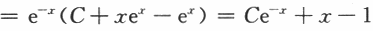
第6题：
第7题：
第8题：
一个测试系统不管其复杂与否，都可以归结为研究输入量x(t)、系统的传输特性h(t)和输出量y(t)三者之间的关系()。
A、y(t)=h(t)*x(t)
B、y(t)=h(t)x(t)
C、y(t)=h(t)/x(t)
D、h(t)=y(t)*x(t)
第9题：
第10题：
。
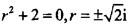