第1题:
求微分方程dy/dx +y=e-x的通解.
第2题:
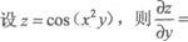
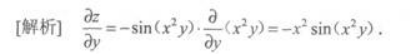
第3题:
求微分方程y″+4y′= 2ex的通解.(6分)

第4题:
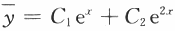
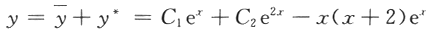
第5题:
 且AB=0,求方程组AX=0的通解.
且AB=0,求方程组AX=0的通解.
第6题:
求xyy=1-x2的通解.
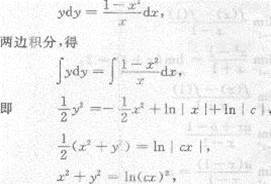
第7题:
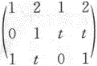 ,且AX=0的基础解系含有两个线性无关的解向量,求AX=0的通解.
,且AX=0的基础解系含有两个线性无关的解向量,求AX=0的通解.
第8题:
求微分方程ex-ydx-dy=0的通解.

第9题:
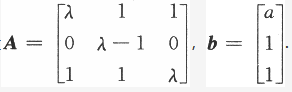
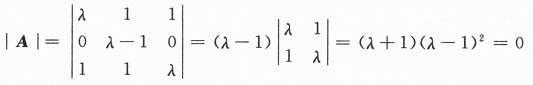

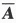 =2,此时方程组无解,λ=1舍去.
=2,此时方程组无解,λ=1舍去.
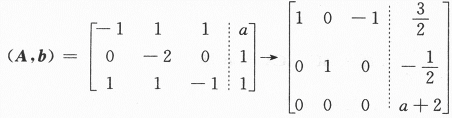

 ,其中k为任意常数
,其中k为任意常数第10题:
 的一个基础解系和通解。
的一个基础解系和通解。