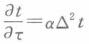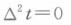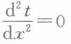某一稳态、常物性、无内热源的导热物体的表面最低温度为100℃,那么其内部绝对不可能出现的温度是()
第1题:
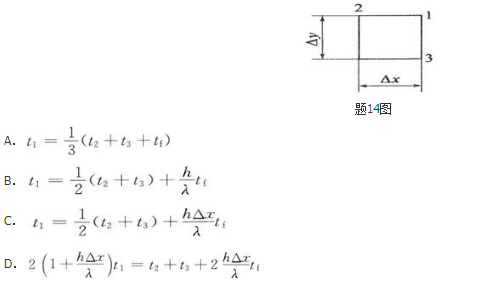
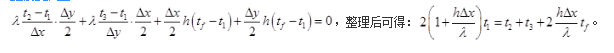
第2题:
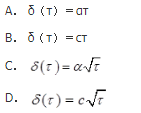
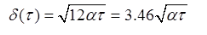
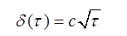
第3题:
A、柱坐标下一维无内热源的不稳态导热微分热方程
B、柱坐标下一维无内热源的稳态导热微分热方程
C、柱坐标下一维有内热源的不稳态导热微分热方程
D、柱坐标下一维有内热源的稳态导热微分热方程
第4题:

第5题:
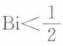
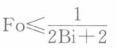
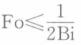
第6题:
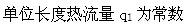
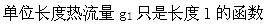

第7题:
第8题:
第一类边界条件下,常物性稳态导热大平壁,其温度分布与导热系数无关的条件是()。
A.无内热源
B.内热源为定值
C.负内热源
D.正内热源
第9题:



第10题: