违法和不良信息举报 联系客服
免费注册 登录

男、女两名田径运动员在长110米的斜坡上练习跑步(坡顶为A，坡底为B)。两人同时从A点出发，在AB之间不停地往返奔跑。如果男运动员上坡速度是3米/秒，下坡速度是5米/秒；女运动员上坡速度是2米/秒，下坡速度是3米/秒，那么两人第二次迎面相遇的地点离A点多少米？（ ）

题目
男、女两名田径运动员在长110米的斜坡上练习跑步(坡顶为A，坡底为B)。两人同时从A点出发，在AB之间不停地往返奔跑。如果男运动员上坡速度是3米/秒，下坡速度是5米/秒；女运动员上坡速度是2米/秒，下坡速度是3米/秒，那么两人第二次迎面相遇的地点离A点多少米？（ ）

如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

甲、乙两人在400米环形跑道上从同一起点反向匀速慢跑，甲的速度为5米/秒，乙的速度为3米/秒，则甲、乙两人经过 再次在起跑点相遇。

A.4分10秒
B.5分50秒
C.6分40秒
D.7分30秒

答案：C
解析：
第一步，本题考查行程问题，属于相遇追及类。
第二步，要使甲乙再次在起跑点相遇，则甲跑过的距离一定为400的整数倍，设甲跑了n圈，所用时间为t，可得5t＝400n，故时间t一定为80的倍数，四个选项的时间分别为250秒、350秒、400秒和450秒，只有C选项符合。
因此，选择C选项。

第2题：

男、女两名田径运动员在长110米的斜坡上练习跑步(坡顶为A，坡底为B)。两人同时从A点出发，在A、B之间不停地往返奔跑。如果男运动员上坡速度是3米/秒，下坡速度是5米/秒；女运动员上坡速度是2米/秒，下坡速度是3米/秒，那么两人第二次迎面相遇的地点离A点多少米？（ ）


答案：B
解析：
本題可以采用逐段分析的方法求解，分别求出第一次相遇点C和第二次相遇点D （见下图）。但是，如果注意到男上坡速度与女下坡速度相同，就可以巧妙地简化解题过程。

如下图所示，将延长一倍到B'，即AB=AB'。男跑的路程相当于从A到B'，再从B'到第二次相遇点D。因为AB=AB'且女下坡速度与男上坡速度相等，所以男到B'点时女恰好到B点。这样一来，求第二次相遇地点的问题，就变成了女从B、男从B'同时出发相向而行的相遇问題。

第3题：

河道赛道长120米，水流速度为2米／秒，甲船速度为6米／秒，乙船速度为4米／秒。比赛进行两次往返，甲、乙同时从起点出发，先顺水航行，问多少秒后甲、乙船第二次迎面相遇?( )


A. 48
B. 50
C. 52
D. 54

答案：C
解析：
解题指导： 因甲的速度快于乙，所以甲、乙第一次迎面相遇时甲逆流，乙顺流。第一次迎面相遇用时：120/V(甲顺）+[120-120V(乙顺）/V(甲顺)]/V(甲逆）+V（乙逆）=15+30/(4+6)=18秒，甲、乙第二次迎面相遇时，甲顺流，乙逆流，第二次相遇用时：15+30+[125-25*V(乙逆）]/[V(甲顺)+V(乙顺）]=45+70/(8+2)=52秒，故答案为C。

第4题：

河流赛道长120米，水流速度2米/秒，甲船速度为6米/秒，乙船速度为4米/秒。比赛进行两次往返，甲、乙同时从起点出发，先顺水航行，问多少秒后甲、乙船第二次迎面相遇？

A. 48
B. 50
C. 52
D. 54

答案：C
解析：
甲回到原地花了15+30=45秒,这时乙到对岸往回走，距离甲为120-（4-2）*（45-20）=70米 甲从原地再出发到相遇的时间为 70/（8+2）=7秒。 所以总时间为45+7=52秒。故答案为C。

第5题：

男、女两名田径运动员在长110米的斜坡上练习跑步(坡顶为A，坡底为B)。两人同时从A点出发，在AB之间不停地往返奔跑。如果男运动员上坡速度是3米/秒，下坡速度是5米/秒；女运动员上坡速度是2米/秒，下坡速度是3米/秒，那么两人第二次迎面相遇的地点离A点多少米？（ ）


答案：B
解析：
本题可以采用逐段分析的方法求解，分别求出第一次相遇点C和第二次相遇点D (见下图)。但是，如果注意到男上坡速度与女下坡速度相同，就可以巧妙地简化解题过程。

第6题：

一个山丘的形状如下图所示。甲乙两人同时从A点出发匀速前往B点，到达B点后立刻返回。甲上坡速度为3米/秒，下坡速度为5米/秒，乙上坡速度为2米/秒，下坡速度为3米/秒。问两人首次相遇时，距A点的路程为多少米？


A.108
B.138
C.150
D.162

答案：B
解析：
第一步，本题考查行程问题。
第二步，计算甲从A到B的时间为120÷3＋60÷5＝52（秒），乙从A到B的时间为120÷2＋60÷3＝80（秒）。这就说明当甲到达B地时乙还在上坡路段行驶，当时间为60秒时，乙到达坡顶，这时甲已开始往回走，甲回程上坡的路程为3×（60－52）＝24（米），这时甲乙相距60－24＝36（米），接着甲乙会首次相遇。
第三步，根据相遇公式，36＝（3＋3）×t，解t＝6（秒），那么可以计算出乙从坡顶行走的距离为3×6＝18（米），这时乙行走的总路程就是两人首次相遇时距离A点的路程，为120＋18＝138（米）。

第7题：

甲、乙两人从相距600米的A、B两地同时出发，相向而行，到达A、B地以后立即返回，如此反复。已知甲的速度为9米／秒，乙的速度为6米／秒，两人每次相遇以后速度增加一倍，则117秒内两人会相遇多少次？( )

A.3
B.4
C.5
D.6

答案：C
解析：
甲、乙两人第一次相遇花了600÷(9+6)=40秒，第一次到第二次相遇之间的路程和为2个AB全程.速度和为第一次相遇的2倍，花了600×2÷(9×2+6×2)=40秒，以后每次相遇的路程和均为2个AB全程.速度和为前一次相遇的2倍，因此相遇时间为前一次相遇时间的一半，117=40+40+20+10+5+2，最后的2秒小于5÷2=2.5，两人并没有相遇，因此相遇次数应该为5次。

第8题：

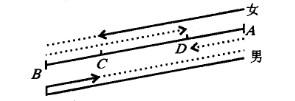
河道赛道场长120米，水流速度为2米／秒，甲船速度为6米／秒，乙船速度为4米／秒。比赛进行两次往返，甲、乙同时从起点出发，先顺水航行，问多少秒后甲、乙船第二次迎面相遇？( )

A．48

B．50

C．52

D．54


正确答案：C
95.C【解析】甲船顺水速度为2+6=8米／秒，逆水速度为6-2=4米／秒；乙船顺水速度为2+4=6米／秒-逆水速度为4-2=2米／秒。笫二次相遇，甲、乙共航行了4倍的赛道长度，甲航行两倍的赛道长度用时120÷8+120÷4=45秒，乙航行一倍的赛道长度用时120÷6=20秒。甲顺水、乙逆水航行的时候第二次相遇，当甲恰好从起点要开始顺水行驶的时候，乙已经逆水航行了2× (45-20) =50米，则乙距起点120-50 = 70米，此时甲乙相遇用时70÷(8+2)=7秒，共用时45+7=52秒，故选C。

第9题：

甲乙两人在一条椭圆形田径跑道上练习快跑和慢跑，甲的速度为3米／秒，乙的速度为7米／秒，他们在同一点同向跑步，经过100秒第一次相遇，若他们反向跑，多少秒后第一次相遇?（ ）

A．30

B．40

C．50

D．70


正确答案：B
根据已知条件，甲乙在同一点同向跑步，经100秒第一次相遇，这属于追击问题。由公式：环形周长＝(大速度－小速度)×同向运动两人两次相遇时间间隔。我们可以求出这条跑道的周长：l00×(7－3)＝400米，那么若甲、乙朝相反方向跑时，属于相遇问题，由公式：环形周长＝(大速度＋小速度)×相向运动两人两次相遇时间间隔。此时的相遇时间为400÷(7+3)＝40秒。故选B。

相关内容