第1题:
随机变量X的均值为5,标准差也为5,随机变量Y的均值为9,方差为16,则V=2X +3Y的均值与方差分别为( )。
A.22;164
B.22;244
C.37;164
D.37;244
第2题:
设X1,X2,…,Xn是一个样本,样本的观测值分别为x1,x2,…,xn,则样本方差s2的计算公式正确的有( )。

第3题:
设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则y=4X1+2X2的均值与方差分别为( )。
A.E(y)=4
B.E(y)=20
C.var(y)=14
D.var(y)=24
E.var(y)=15
第4题:
第5题:
第6题:
设两个相互独立的随机变量X,Y方差分别为6和3,则随机变量2X-3Y的方差为()
A、51
B、21
C、-3
D、36
第7题:
第8题:
设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则Y=4X1-2X2的均值与方差分别为( )。
A.E(Y)=4
B.E(Y)=20
C.Var(Y)=8
D.Var(Y)=14
E.Var(Y)=24
第9题:

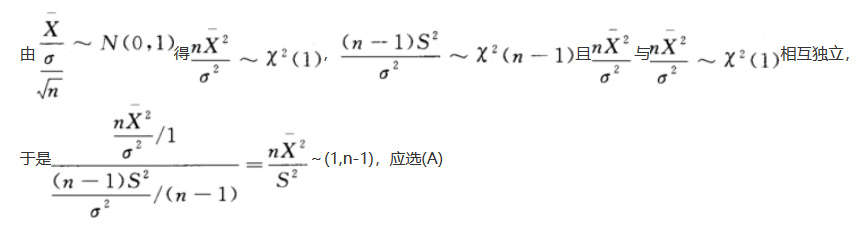
第10题: