(-2,2)
(-2,4)
(0,4)
(-4,0)
第1题:
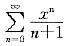 的收敛域为( )。
的收敛域为( )。 ,当x=1,级数
,当x=1,级数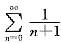 发散,当x=-1,级数
发散,当x=-1,级数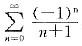 ,由莱布尼兹定理知它收敛,因而收敛域为[-1,1)
,由莱布尼兹定理知它收敛,因而收敛域为[-1,1)第2题:

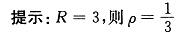
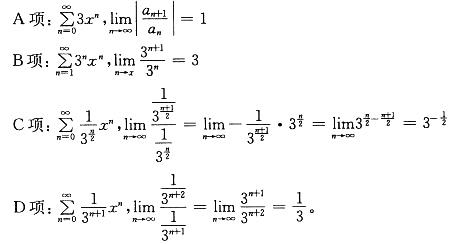
第3题:
将函数f(x)=1/(3-x)展开成(x+1)的幂级数并指出收敛区间(6分)
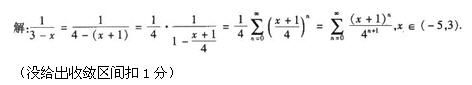
第4题:
 的收敛半径为
的收敛半径为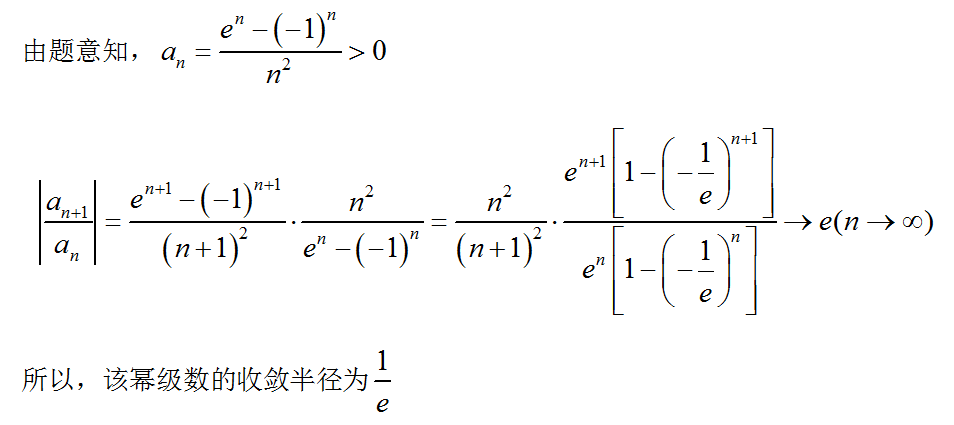
第5题:
 的收敛区间是:
的收敛区间是:
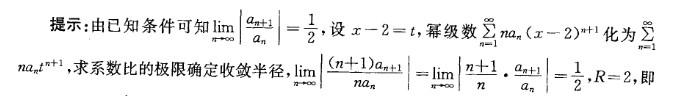
第6题:
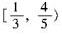

第7题:
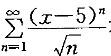 在其收敛区间的两个端点处如何敛散?
在其收敛区间的两个端点处如何敛散?
 求出R=1,即 z
求出R=1,即 z第8题:
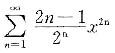 的收敛域为( )。
的收敛域为( )。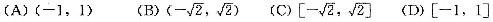
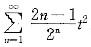
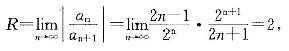 当|t|<2,即|x2|<2,亦即
当|t|<2,即|x2|<2,亦即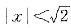 时收敛,而当
时收敛,而当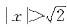 发散,而当
发散,而当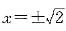 时,级数∑(2n-1)发散,从而原级数的收敛域为
时,级数∑(2n-1)发散,从而原级数的收敛域为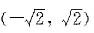
第9题:
 则所得级数的收敛半径R等于:
则所得级数的收敛半径R等于:
 D.R 值与 a、b 无关
D.R 值与 a、b 无关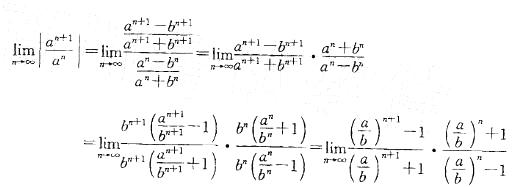
第10题:
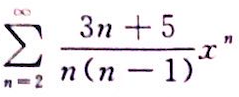 的收敛域与和函数.
的收敛域与和函数.