用回溯法解0/1背包问题时，该问题的解空间结构为（）结构。
第1题：
不能保证求得0-1背包问题的最优解。
A．分支限界法
B．贪心算法
C．回溯法
D．动态规划策略
第2题：
利用贪心法求解0/1背包问题时，(55)能够确保获得最优解。用动态规划方法求解 0/1背包问题时，将“用前i个物品来装容量是X的背包”的0/1背包问题记为KNAP(1,i,X)，设fi(x)是KNAP(1,i,X)最优解的效益值，第j个物品的重量和放入背包后取得效益值分别为 wj和pj(j=1～n)。则依次求解f0(x)、f1(x)、...、fn(X)的过程中使用的递推关系式为(56)。.
A．优先选取重量最小的物品
B．优先选取效益最大的物品
C．优先选取单位重量效益最大的物品
D．没有任何准则
第3题：
此题为判断题(对，错)。
第4题：
● （65） 不能保证求得0-1 背包问题的最优解。
（65）
A. 分支限界法
B. 贪心算法
C. 回溯法
D. 动态规划策略
第5题：
利用贪心法求解0/1背包问题时，(26)能够确保获得最优解。用动态规划方求解O/1背包问题时，将“用前i个物品来装容量是x的背包”的0/1背包问题记为KNAP(1，i，X)设fi(X)是KNAP(1，i，X)最优解的效益值，第j个物品的重量和放入背包后取得效益值分别为W和p(j=1～n)，则依次求解f0(X)，f1(X)，…，fn(X)的过程中使用的递推关系式为(27)。
A．优先选取重量最小的物品
B．优先选取效益最大的物品
C．优先选取单位重量效益最大的物品
D．没有任何准则
第6题：
回溯法也称为试探法。以下关于回溯法的结论中正确的是(50)。
A．即使问题的解存在，回溯法不一定能找到问题的解
B．回溯法找到的问题的解不一定是最优解
C．回溯法不能找到问题的全部解
D．回溯法无法避免求出的问题解的重复
第7题：
0-1背包问题可以描述为：有n个物品，对i=1，2，…，n，第i个物品价值为vi ，重量为wi（vi，和wi为非负数），背包容量为W（W为非负数），选择其中一些物品装入背包，使装入背包物品的总价值最大，
，且总重量不超过背包容量，即
，其中，xi∈{0,1}，xi=0表示第i个物品不放入背包，xi=1表示第i个物品 放入背包。
【问题1】（8分）
用回溯法求解此0-1背包问题，请填充下面伪代码中（1）~（4）处空缺。
回溯法是一种系统的搜索方法。在确定解空间后，回溯法从根结点开始，按照深度优先策略遍历解空间树，搜索满足约束条件的解。对每一个当前结点，若扩展该结点己经不满足约束条件，则不再继续扩展。为了进一步提高算法的搜索效率，往往需要设计一个限界函数，判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND（v,w,k,W）函数，其中v, w, k和W分别表示当前已经获得的价值、当前背包的重量、己经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点，该函数值表示确定了部分物品是否选择之后，对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值，若该价值小于等于当前已经得到的最优解，则该结点无需再扩展。
下面给出0-1背包问题的回溯算法伪代码。
函数参数说明如下：
W：背包容量；n：物品个数；w：重量数组；v：价值数组；fw：获得最大价值时背包的重量；fp：背包获得的最大价值；X：问题的最优解。
变量说明如下：
cw：当前的背包重量；cp：当前获得的价值；k：当前考虑的物品编号；Y：当前已获得的部分解。
BKNAP(W,n,w,v,fw,fp,X）
1 cw ← cp ← 0
2 （1）
3 fp ← -1
4 while true
5 while k≤n and cw＋w[k]≤W do
6 （2）
7 cp ← cp＋v[k]
8 Y[k]← 1
9 k ← k+1
10 if k＞n then
11 if fp＜cp then
12 fp ← cp
13 fw ← ew
14 k ← n
15 X ← Y
16 else Y(k)← 0
17 while BOUND(cp,cw,k,W) ≤fp do
18 while k≠0 and Y(k)≠1 do
19 （3）
20 if k＝0 then return
21 Y[k]←0
22 cw ← cw ← w[k]
23 cp ← cp ← v[k]
24 （4）
本题考查的是用回溯法求解0-1背包问题。回溯法有两类算法框架：非递归形式和递归形式，本题采用非递归形式表示。理解回溯法的基本思想和这两类算法框架是正确解答本题的根本要求·回溯法从第一项物品开始考虑是否应该装入背包中，因此当前考虑的物品编号k从1开始，即k←1。然后逐项往后检查，若能全部放入背包则将该项放入背包，此时背包的重量应该是当前的重量加上当前考虑物品的重量，即cw←cw+w[k]，当然背包中物品的价值也为当前的价值加上当前考虑物品的价值。若己经考虑完了所有的物品，则得到一个解，判断该解是否为当前最优，若为最优，则将该解的信息放入变量fp、fw和X中。若还没有考虑完所有的物品，意味着有些物品不能放入背包，此时先判断若不将当前的物品放入背包中，则其余物品放入背包是否可能得到比当前最优解更优的解，若得不到则回溯；否则继续考虑其余的物品。
【问题1】（共8分，各2分）
（1）k ← 1 或其等价形式
（2）cw ← cw + w[k] 或其等价形式
（3）k ← k – 1 或其等价形式
（4）k ← k + l 或其等价形式
第8题：
A.多重解
B. 无解
C. 退化解
D. 无穷多最优解
第9题：
【问题 1】（8 分）
用回溯法求解此 0-1 背包问题，请填充下面伪代码中（1）～（4）处空缺。
回溯法是一种系统的搜索方法。在确定解空间后，回溯法从根结点开始，按照深度优先策略遍历解空间树，搜索满足约束条件的解。对每一个当前结点，若扩展该结点已经不满足约束条件，则不再继续扩展。为了进一步提高算法的搜索效率，往往需要设计一个限界函数，判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND( v,w,k,W )函数，其中 v、w、k 和 W分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点，该函数值表示确定了部分物品是否选择之后，对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值，若该价值小于等于当前已经得到的最优解，则该结点无需再扩展。
下面给出 0-1背包问题的回溯算法伪代码。
函数参数说明如下:
W：背包容量；n：物品个数；w：重量数组；v：价值数组；fw：获得最大价值时背包的重量；fp：背包获得的最大价值；X：问题的最优解。
变量说明如下：
cw：当前的背包重量；cp：当前获得的价值；k：当前考虑的物品编号；Y：当前已获得的部分解。
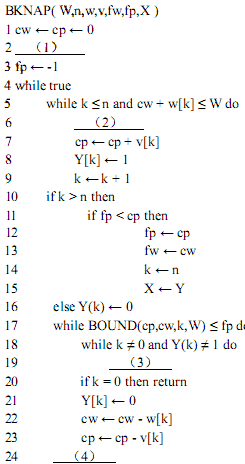
第10题：
0-1背包问题的回溯算法所需的计算时间为（），用动态规划算法所需的计算时间为（）。