有4个不同的自然数，他们当中任意两数的和是2的倍数，任意3个数的和是3的倍数，为了使这4个数的和尽可能小，则这4个数的和为（）
第1题：
A、其中最少有两个数的差是4的倍数
B、其中最少有两个数的差是5的倍数
C、其中最少有两个数的差是6的倍数
D、其中最少有两个数的差是7的倍数
第2题：
此题为判断题(对，错)。
第3题：
一个小于60的自然数与3的和是5的倍数，与3的差是6的倍数，这个数最大是多少?（ ）
A．47
B．51
C．52
D．57
第4题：
从1，2，3，……，50这五十个数中，取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取多少个数( )。
A. 21 B. 22C. 23 D. 29
从0开始，每7个数一组（0——6，7——13，......，42——48，共七组）中，最多可以选4个数（分别是除7余0，1，2，3的数）
所以，它们之中可以选7*4＝28个数。
另外：0不包含在其中，要减去1个数；49和50两个数除7的余数分别是0和1，也要计算上，再加2个数。
故，最多共可取28－1+2＝29个数
第5题：
有一串自然数，已知第一个数与第二个数互质，而且第一个数的5/6恰好是第二个数的1/4，从第三个数开始，每个数字正好是前两个数的和，问这串数的第2005个数被3除所得的余数是（ ）。
A．2
B．1
C．0
D．3
等于第二个数的
，则可知第一个数与第二个数之比为3：10，由于这两个数互质，所以第一个数为3，第二个数为10，从而这串数为3，10，13，23，36，59，95，154，249，403，652，1055，…，这一数列被3除的余数是：0，1，1，2，0，2，2，1，0，1，1，2，…，按“0，1，1，2，0，2，2，1”循环。因为2005÷8＝250…5，所以第2005个数被3除所得的余数应该是第251个周期中的第5个数，即0。
第6题：
从1、2、3、4、5、6、7、8、9中任意选出三个数，使它们的和为奇数，共有多少种不同的选法?
A．44
B．43
C．42
D．40
[答案]D。[解析]若使三个数的和为奇数，必须三个数同为奇数或两个为偶数、一个为奇数。三个数都是奇数时，从5个奇数中选3个，共有种选法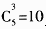
；两个数为偶数、1个数为奇数时，从四个偶数中选出2个，再从5个奇数中选出一个，共有种选法
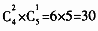。总共30+10=40种选法。
第7题：
有四个不同的正整数，其中任意两个数之和是2的倍数，任意三个数的和是3的倍数，满足条件的最小的四个正整数之和是：
A．51
B．38
C．40
D．42
第8题：
任意两个自然数中一定有一个是奇数。（ ）
第9题：
从1，2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为（ ）。
A．134
B．267
C．316
D．133
第10题：
从1、2、3、4、5、6、7、8、9中任意选出三个数，使它们的和为奇数，共有( ) 种不同的选法。
A．44
B．43
C．42
D．40